こんにちは、まぐろです。
今回は定義域・値域・変域について解説します。
似た名前ですし、それぞれが同じようなものを表しています。
混同しないように、注意して理解していきましょう。
定義域、値域、変域の定義
定義域とは
それでは、まず定義域について説明していきます。
定義域とは、1次関数(に限らず任意の関数)において、\(x\)の値が取りうる領域のことです。
例えば、\(y=2x+1\)の\(x\)が取りうる値の領域が\(-2 \le x \le 2\)であるとき、\(x\)の定義域は \(-2 \le x \le 2\) であるといえますね。
値域とは
では、次に値域についてですが、これはyの値が取りうる範囲のことです。
なので、\( y=2x+1\)の\(y\)が取りうる値の領域が\(-3 \le y \le 5\)であるとき、\(y\)の値域は \(-3 \le y \le 5\) であるといえます。
変域とは
最後に、変域はなにかというと、これは定義域と値域を合わせたもののことを指します。
例として、 \( y=2x+1\)が取りうる値の領域が\(-2 \le x \le 2\)、 \(-3 \le y \le 5\) であるとき、\(x\), \(y\)の変域は\(-2 \le x \le 2\)、 \(-3 \le y \le 5\) であるといえます。
この記事では以降、変域という言葉に統一して説明を進めていきます。
変域の求め方
変域の計算手順を確認してみましょう。
変域を計算するためには、グラフの概形をイメージできるよう方が良いので、1次関数の概形がイメージできない人は、まずそこから練習しましょう。
実際の計算手順は以下になります。
- 1次関数の概形をイメージする。
- グラフの最大値と最小値をグラフの形を見て決定する。
- その時の値を計算して求める。
計算例
1次関数\(y=2x-1\) (\(-2 \le x \le 2\))の\(y\)の変域を求める。
ではまず、グラフの概形をイメージしてみましょう。
こんな感じですね。
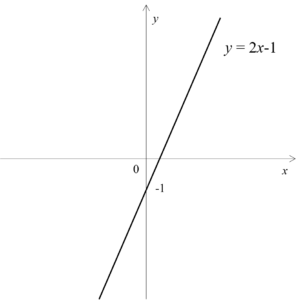
この例題では\(x\)の変域が与えられているので、 \(x\)の変域を満たすようグラフを書き直してみましょう。
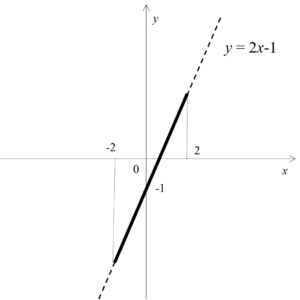
するとこんな感じになりますね。
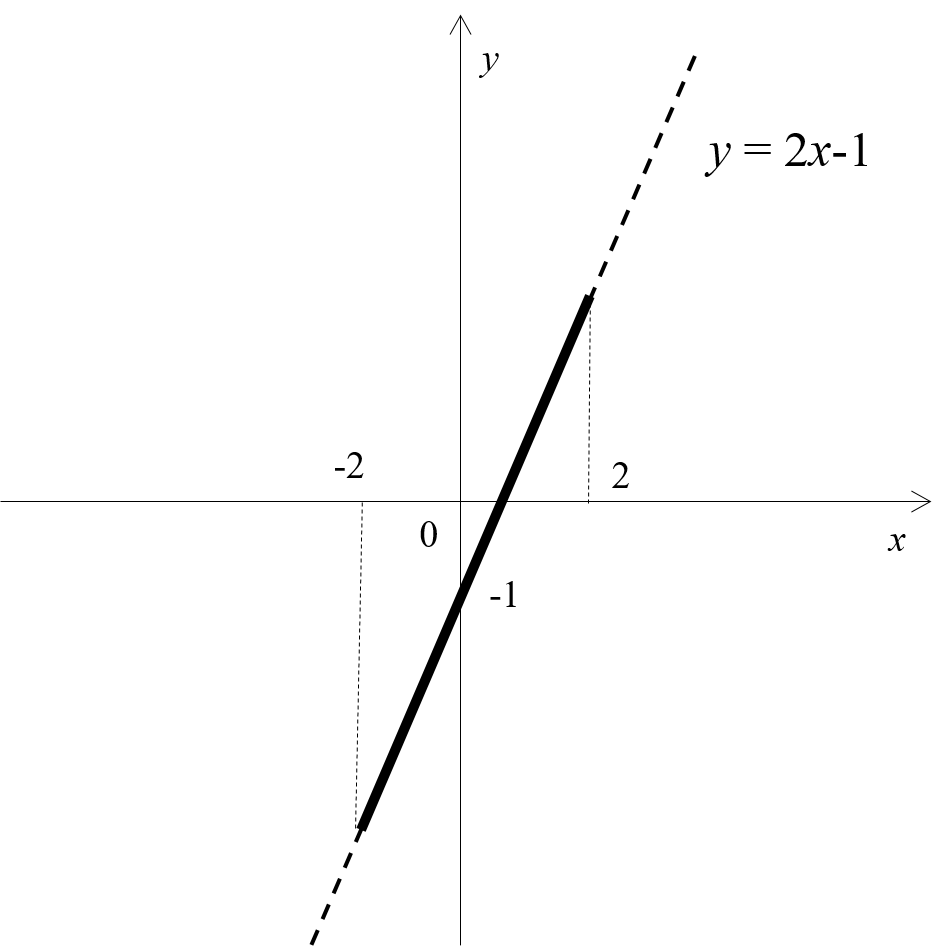
さて、グラフを見ると、\(y\)の最大値は\(x=2\)のとき、最小値は\(x=-2\)のときにとっていることがわかりますね。
ではまず、\(y\)の最大値から求めてみましょう。\(x=2\)のときの\(y\)の値は…
\(y=2x-1=2 \times 2 – 1=4-1=3\)
となります。
次に、\(y\)の最小値を求めてみましょう。\(x=-2\)のときの\(y\)の値は…
\(y=2x-1=2 \times (-2) – 1=-4-1=-5\)
となります。
最後に答えとして不等号の形で表せばよいので、
\(-5 \le y \le 3\)
と答えが求まります。
まとめ
今回は定義域・値域・変域の違いとその計算方法について解説しました。
実際に変域を求める際にはグラフの概形もイメージできる必要があるので、併せて勉強していきましょう。

コメント