こんにちは、まぐろです。
今日は1次関数における切片について解説を行います。
1次関数の切片がわからない。傾きと何が違うのか知りたいという方は読んでみてください。
1次関数の切片とは
切片の定義
そもそも切片とは何か。といいますと、グラフと座標軸の交点のことをいいます。
特に、中学数学の1次関数で「切片」というと、y軸とグラフとの交点のことを指しています。
下図でいう赤丸のところですね。

数式でいうと…
切片は一次関数の式でいうとどこに相当するのでしょうか。
実は一次関数の式 \(y=ax+b\) の \(b\) が切片に相当します。
では、なぜ \(b\) が切片に相当するのかを考えていきましょう。
切片の定義を思い出してもらうと、切片というのはy軸とグラフとの交点を表していると定義されています。
ここで、「y軸」というのはどういう性質を持っているかというと、y軸はすべてのx座標が0となっているという性質を持っています。
そこで、1次関数の式に\(x=0\)を代入すると、
\(y=a \times 0 + b = b\)
となり、\(b\) だけが残ります。
そのため、1次関数の式中の\(b\)が切片に相当するのです。
傾きとの違い
では、切片と傾き(変化の割合)の違いは何でしょうか。
切片は上記で述べたように、グラフとy軸との交点を表しています。
傾きは何を表しているかというと、グラフの傾き具合・急さを表しているのでした。
つまり、切片・傾きはそれぞれ違うものを表していますが、どちらもグラフの形状を表すのに必要な要素ということですね。
なお、一次関数の式 \(y=ax+b\) で表すと、傾きは \(a\)、切片は \(b\)にそれぞれ相当します。
このあたりはきちんと整理して覚えておきたいですね。
切片の求め方
数式から求める場合
ではまず、数式から切片を求める方法を考えてみましょう。
上の方で述べた通り、切片というのは一次関数の式でいう \(b\) のことでした。
つまり、1次関数の式さえわかっていたらあとは \(b\) の値を見るだけで答えがわかるというわけです。
グラフから求める場合
次に、一次関数の式がわかっていないが、グラフの形がわかっている場合について考えてみましょう。
例として、下図のようなグラフの切片を求めたい場合、見るべきはy軸とグラフとの交点です。

図からこの場合の切片は「-2」だとわかります。
この例の場合でも、見るべきところを知っていればすぐに答えを求めることができますね!
計算例
グラフから求める例は上で例を示したので、数式から切片を求める例を説明します。
\(y=2x-5\)の切片を求める。
数式がわかっている場合、\(y=ax+b\) の \(b\) に当たるところが切片に相当するのでした。
この例題の場合、\(b\) にあたるところは「-5」になっています。
つまり、この1次関数の切片は「-5」ということがわかります。
まとめ
今回は1次関数の切片について説明しました。
切片は求め方を知っていれば比較的簡単に求めることができます。
変化の割合と合わせて、得点できるようにしておきたいですね!
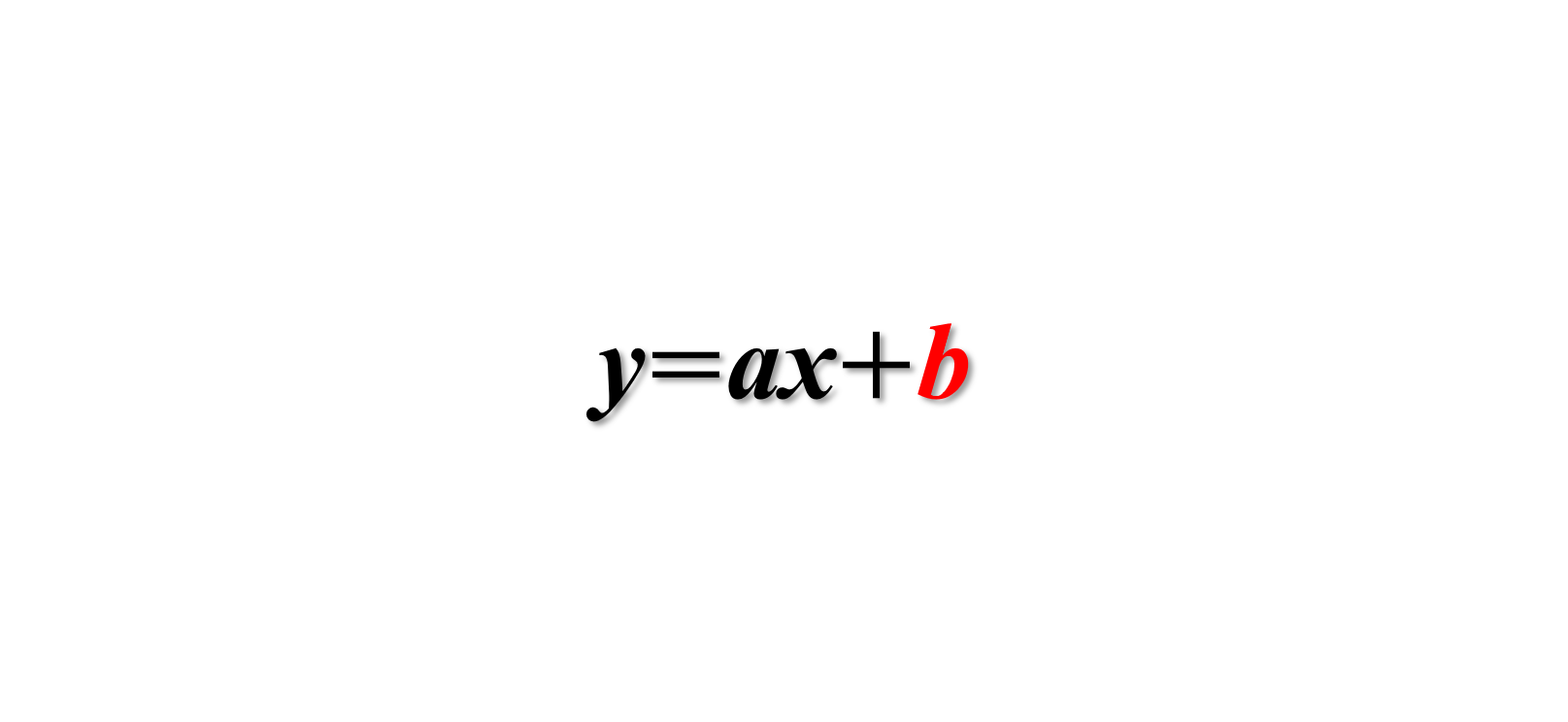

コメント