こんにちは、まぐろです。
前回に引き続き、一次関数の変域を使った問題の解説をしていきます。
前回はちょうど切片を通るような変域でしたが、今回はより一般的な問題です。
例題
\(a \lt 0\)である一次関数\(y=ax+b\)において、\(x\)の変域が\(1 \le x \le 3\), \(y\)の変域が\(-1 \le y \le 3\)であるとき、\(a, b\)の値を求めよ。
さて、このような例題が与えられたとき、まず何をすればよいかというと、問題のゴールを見つけてそこに至るまでの方法を考えます。
今回の問題では、問題のゴールは\(a, b\)の値を求めることです。
値を求めるためになにをすればよいかというと、変域の関係から一次関数の端の点を2点見つければよさそうです。
さらに、2点を見つけるためには、\(a\)の値からグラフの形を考えるのがよさそうです。
つまり、この問題を解くために必要な手順は上で述べたことを逆に行えばよいので、このようになります。
- 一次関数の形を考える
- 一次関数の両端の点を見つける
- \(a, b\)の値を求める
一次関数の形を考える
まずは一次関数の形を考えましょう。
一次関数の形をイメージするのに一番大切な項目は傾きです。
傾きの正負によってグラフが右上がりになるか、右下がりになるかが決定します。
つまり、傾きによって一次関数の端となる点の組み合わせが変わってくるのです。
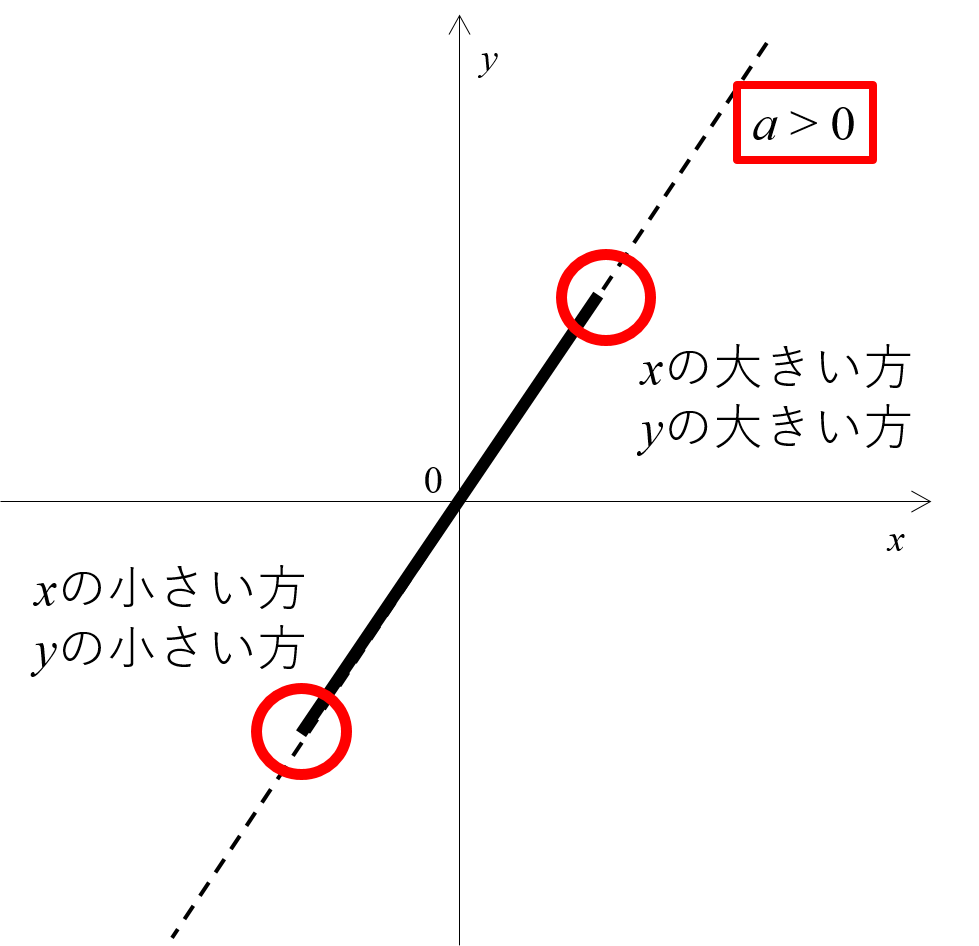
図に示す通り、傾きが正のときは\(x\)が大きい方と\(y\)が大きい方、\(x\)が小さい方と\(y\)が小さい方がペアになります。
ところが、傾きが負のときは逆になり、\(x\)が大きい方と\(y\)が小さい方、\(x\)が小さい方と\(y\)が大きい方のペアになります。
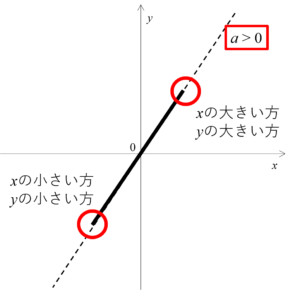
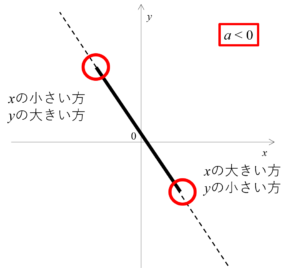
今回は問題文に\(a \le 0\)と書いてあるので、下の図のパターンであることがわかります。
一次関数の両端の点を見つける
先ほどの傾きの話から、\(x\)の大きい方と\(y\)の小さい方、\(x\)の小さい方と\(y\)の大きい方がそれぞれペアであることがわかりました。
つまり、今回の変域でいうと、\(x=3, y=-1\)のペアと\(x=1, y=3\)のペアがそれぞれ一次関数の端の点に相当します。
一次関数の式を求める
ここまでくれば、あとは2点を通る一次関数を求める問題だということができます。
つまり、初めの例題を、「\(x=3, y=-1\)、\(x=1, y=3\)を通る一次関数を求めよ。」と簡単に言い換えることができたことになります。
この問題の解き方は以前の記事で解説しています。
なので、1通りの解き方でしかここでは解説しません。
\(x=3, y=-1\)を変化前の点、\(x=1, y=3\)を変化後の点だとすると、\(xの増加量は\)、
\(x\)の増加量\(=1-3=-2\)
また、\(y\)の増加量は、
\(y\)の増加量\(=3-(-1)=4\)
となるため、変化の割合は、
変化の割合=\( \displaystyle \frac{4}{-2}=-2\)
さらに、\(x=1, y=3\)をもとの式に代入すると、
\(3 = -2 \times 1 + b\)
\(b=3 + 2=5\)
となるので、求める一次関数は\(y=-2x+5\)であるとわかります。
まとめ
今回も、変域を使った一次関数の求め方について解説しました。
新しく出てきたことは、一次関数の傾きによって、端の点をとる\(x, y\)の組み合わせが変わってくるということだけです。
\(x, y\)の組み合わせさえ求めてしまえば、あとはこれまでの知識をつかうことで問題を解くことができます。
一次関数の問題が難しく見えても、ひとつずつ見ていけば案外何とかなるものです。
一次関数の勉強頑張っていきましょう。
それでは。
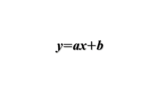

コメント