こんにちは、まぐろです。
今日は1次関数の変化の割合を解説します。
変化の割合がわからないよ!って人はぜひ読んでいってみてくださいね。
変化の割合とは
定義
まず初めに、変化の割合の定義について説明します。
1次関数の式が \(y=ax+b \)で表されたとき、変化の割合はこの式の\(a\)の部分が相当します。
この変化の割合は次のように定義されています。
$$a=\displaystyle \frac{yの増加量 }{xの増加量 }$$
残念ながら、この定義は覚えるしかないですね。
逆に言えばこの式さえ覚えていれば、他に暗記しなければいけないことはほとんどありません。(いろいろと理解は必要ですが。)
変化の割合の意味
では、この変化の割合は何を意味しているのでしょうか。
定義にあるように、yの増加量をxの増加量で割ると、xが1進んだときにyがいくつ増えるかを表します。
変化の割合は下の図中での「?」の量を表します。
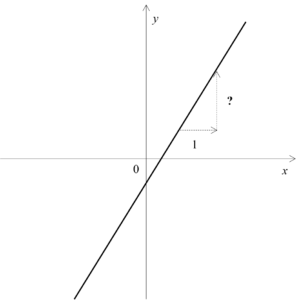
ここで、図を見ると、「?」つまり変化の割合の部分が大きくなればなるほど、グラフの傾きが急になりそうだということが確認できますね。
実は、変化の割合と傾きは同じものを表しています。
問題文中でどちらの表現が現れても、頭の中で読み替えができるようになっておきたいですね。
変化の割合の求め方
計算例
ここでは簡単な例をつかって、いくつかの例題を解いてみたいと思います。
(1) xの増加量が3, yの増加量が9のとき、変化の割合を求める。
(2) 変化の割合が2, xの増加量が3のとき、yの増加量を求める。
(1)
変化の割合の定義に当てはめてみましょう。
\(変化の割合 =\displaystyle \frac{yの増加量 }{xの増加量 }=\frac93=3\)
というわけで、答えは3であるとわかります。
(2)
これも変化の割合の定義式に当てはめてみます。
\(変化の割合=\displaystyle \frac{yの増加量 }{xの増加量 }\)
\(2=\displaystyle \frac {yの増加量 }{3}\)
\(yの増加量=2 \times 3 = 6\)
答えは6だとわかりました。
変化の割合を求める問題は定義を覚えておけば楽に解くことができますね。
まとめ
今回は1次関数の変化の割合の定義と意味について解説しました。
変化の割合はまず定義をしっかり覚えることが大事ですね。
計算例は非常に簡単なもので説明しましたが、もう少し複雑な例もそのうち解説していきたいですね。
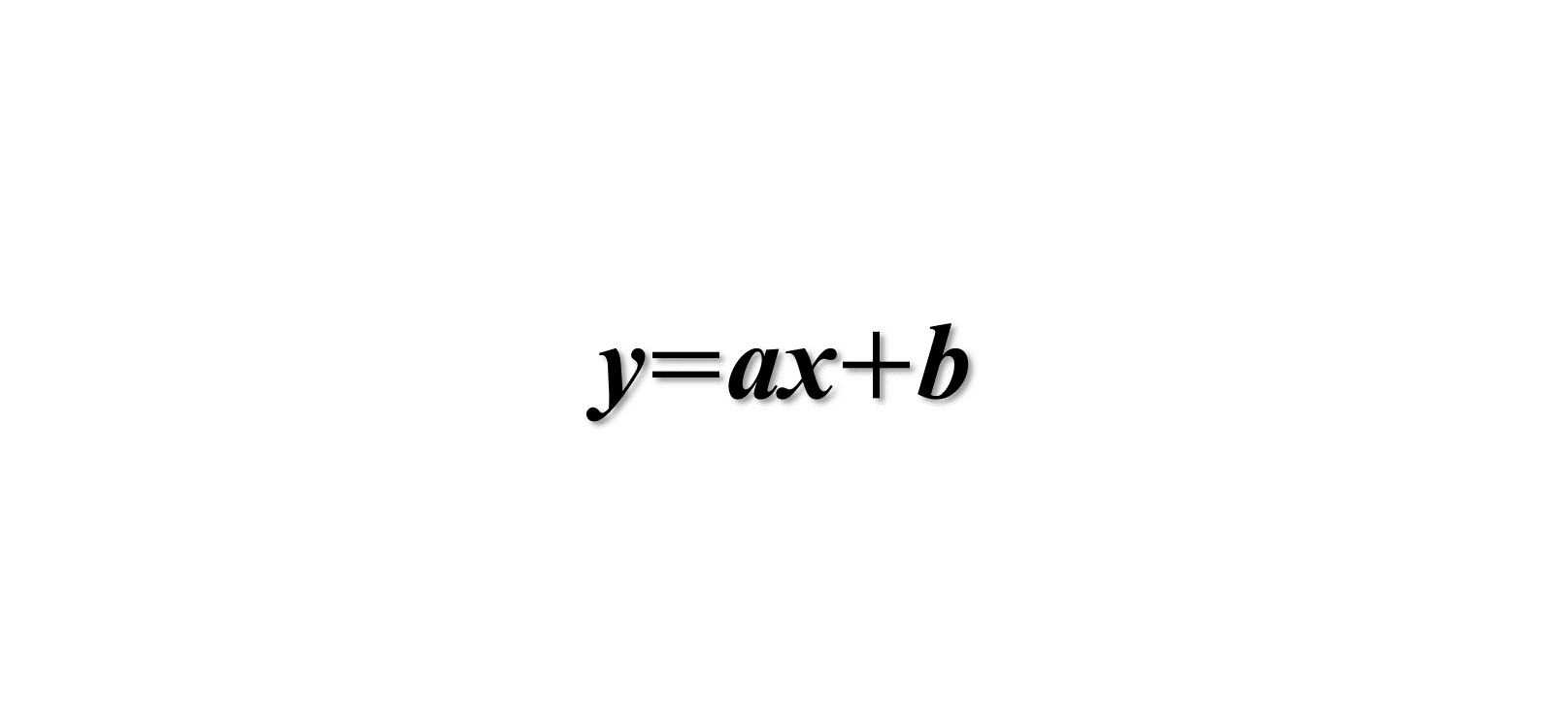

コメント