こんにちは、まぐろです。
今回は一次関数の最大値・最小値の求め方について解説します。
ポイントは一次関数のグラフをちゃんと意識することですね。
最大値・最小値とは
それでは初めに、最大値・最小値とは何かについて確認しておきましょう。
最大値とは文字通り、「最も大きい値」のことをいいますし、最小値とは文字通り「最も小さな値」のことをいいます。
また、基本的に最大・最小値は\(y\)の値について答えることが多く、単に最大・最小値という言葉が現れたら\(y\)の最大・最小値と思っても大丈夫です。
一次関数に関して言うなら、グラフを描いたときに一番高いところにある点が最大値、一番低いところにある点が最小値になります。
これは、先に述べました通り、最大・最小値は基本的に\(y\)の値について考えるからです。
(グラフでは\(x\)が右左を、\(y\)が上下をそれぞれ表していましたね。)
不等号について
最大・最小値について考える際に避けて通れないのが不等号の意味についてです。
「\(\lt\)」と「\(\leq\)」の違いが何かわかるでしょうか。(注:\(\le\)は教科書とかだと下に線が2本ついていると思いますが、表示できなかったので1本線のものを使用しています。)
「\(\lt\)」の方は右の項が左の項よりも大きいということを表しており、「\(\le\)」の方は右の項が左の項以上であるということを表しています。
「より大きい」と「以上」という言葉が出てきましたが、これらの言葉の違いは大きさが同じになることが許されるかどうかです。
「以上」を使うときは、右と左が同じ大きさになってもOKですが、「より大きい」を使うときは右と左が同じ大きさになってはいけません。
「以上」の「以」は「イコール」の「イ」と中学時代に習った記憶がありますが、多少こじつけてでも覚えてしまいましょう。
最大・最小値の求め方
それでは、\(y=x\)という右上がりな一次関数を使って、最大・最小値の求め方を説明します。
先に問題を解く流れを書いておくと、
- グラフの形をイメージ
- どこで最大・最小値を取りうるか考える
- ほんとに最大・最小を取るか考える
の3ステップです。早速見ていきましょう。
グラフの形をイメージ
問題ではたいてい次のような聞かれ方をすると思います。
「\(y=x (-2\le x\lt1)のとき、yの最大値・最小値を求めよ\)」
このとき何を考えればよいかというと、まずはグラフの形をイメージします。
特に、グラフが右上がりなのか、右下がりなのかは必ず考えましょう。
ちなみに、グラフが右上がりなのか右下がりなのかを判断するには傾きの値を使います。
傾きが正なら右上がり、傾きが負なら右下がりでしたね。
どこで最大・最小を取るか考える
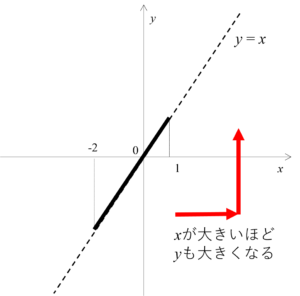
この例の場合、傾きは1なので右上がりのグラフですね。右上がりということは、右に行くほど(=\(x\)が大きくなるほど)\(y\)の値が大きくなるということを表しています。
このことから、\(x=-2\)のとき最小値、\(x=1\)のときに最大値を取りそうですね。
そこで、実際に\(x=-2, 1\)のときの\(y\)の値を求めてみましょう。
\(x=-2のとき、y=-2\), \(x=1のとき、y=1\)となります。
では、これをそのまま答えにしてよいのでしょうか?
本当に最大・最小を取るか考える
実はまだ考えることがあります。\(x\)の変域についてです。
\(xの変域は、-2\le x\lt1\)でした。つまり、\(x\)は-2を含むが1は含まないということを表しています。
ん?難しくなりましたね。まずは、簡単な最小値から考えましょう。
\(xが-2を含むということは、x=-2が成立してよいということを意味します。\)
つまり、\(x\)が-2になることがあるので、最小値は\(x=-2\)のとき\(y=-2\)を取ります。
では、最大値はどうでしょうか。
\(xは1よりも小さいので、1に近づくことはできますが、1になることはありません。\)
つまり、どんどん大きくなる(1に近づく)ことができるのですが、永遠に到達することはできないのです。まさにゴールド・エクスペリエンス・レクイエムのような能力ですね。(わからない人はジョジョ5部を読みましょう)
こういうとき、一番大きい数は?と聞かれても、そのときの\(x\)の値が決まらないので答えようがありません。
そのため、最大値はなしと答えるのが正解です。
あとは、黄色いマーカーの部分を答えて終了です。
まとめ
今回は一次関数の最大値・最小値について解説しました。
ポイントはグラフの形をイメージすることと、\(x\)の変域によっては最大値・最小値が現れないことの2点に気を付けることですね。
最後の最大値・最小値が存在するかどうかは、\(x\)の変域にイコールがついているかどうかで判断すればいいのですが、一度はなぜそうなるのか?を考えると、ただの丸暗記ではない生きた知識として身に着けることができますよ。
それでは。

コメント