こんにちは、まぐろです。
今回は変域を使った問題の解き方を解説します。
問題の文章量が増えてきていますが、少しずつ理解していきましょう。
例題
\(y=ax+3\)において、\(x\)の変域が\(0\le x \le4\)のとき、\(y\)の変域が\(1 \le y \le 3\)である。\(a\)の値を求めよ。
さて、このような問題が現れた時、どう解いていけばよいでしょうか。
ひとつずつ考えていきましょう。
何がわかればよいのか
こういった問題を解くときは、何がわかれば計算して解いていくことができるのかをまず考えましょう。
今回の例題では、\(a\)の値を求めるのがゴールです。
では、\(a\)の値はどうやって求めるのかを考えてみましょう。
\(a\)の値を求めるためには、\(x, y\)の組が一つ分かれば求めることができそうですね。
以上のことをまとめると、次のようになります。
- 変域を使って\(x, y\)の組を見つける
- \(x, y\)の組を式\(y=ax+3\)に代入して\(a\)の値を求める。
変域を考える
着目したいのが\(x, y\)の変域の関係についてです。
つまり、\(x\)がいくつのときに\(y\)がいくつになるか、という関係を見つけましょう。
今回の例題では、\(x\)の変域の端に\(x=0\)があるところに目をつけてみましょう。
なぜ、\(x=0\)に目をつけるのかというと、\(x=0\)のときというのは\(a\)の値によらず\(y\)の値が一定になるからです。(切片のことですね。)
では、\(x=0\)を代入してみましょう。
\(y=ax+3=a \times 0 + 3=3\)
となり、\(y=3\)が得られます。
ここで、\(y\)の変域に着目すると、\(y=3\)がありますね。つまり、\(x=0, y=3\)がこの一次関数が通る一つの点だということがわかります。
もう一方の端に注目する
一次関数は直線ですので、端の点は2点存在します。
先ほどの計算で1点が求まったので、もう1点を求めましょう。
\(x\)の変域が\(0 \le x \le 4\)、\(y\)の変域が\(1 \le y \le 3\)であり、\(x, y\)の組のうち一つは\(x=0, y=3\)であることがわかりました。
ここから、端のもう1点は\(x=0\)じゃない方と\(y=3\)じゃない方の組み合わせ、つまり、\(x=4, y=1\)であるとわかります。
では、この組を一次関数の式に代入してみましょう。
\(y=ax+3\)
\(1=a \times 4+3\)
\(4a=-2\)
\(a=-\displaystyle \frac {1}{2}\)
見事に\(a\)の値が出てきましたね。
よって、答えは\(\displaystyle y = -\frac{1}{2} x+3\)とわかります。
まとめ
一次関数の変域を使った式の求めかたは、変域の端に注目して一次関数が通る点を求めるのがポイントです。
また、今回は切片の条件から一次関数を求めましたが、次回は傾きの条件から一次関数を求める問題の解説をしていきたいですね。
それでは、
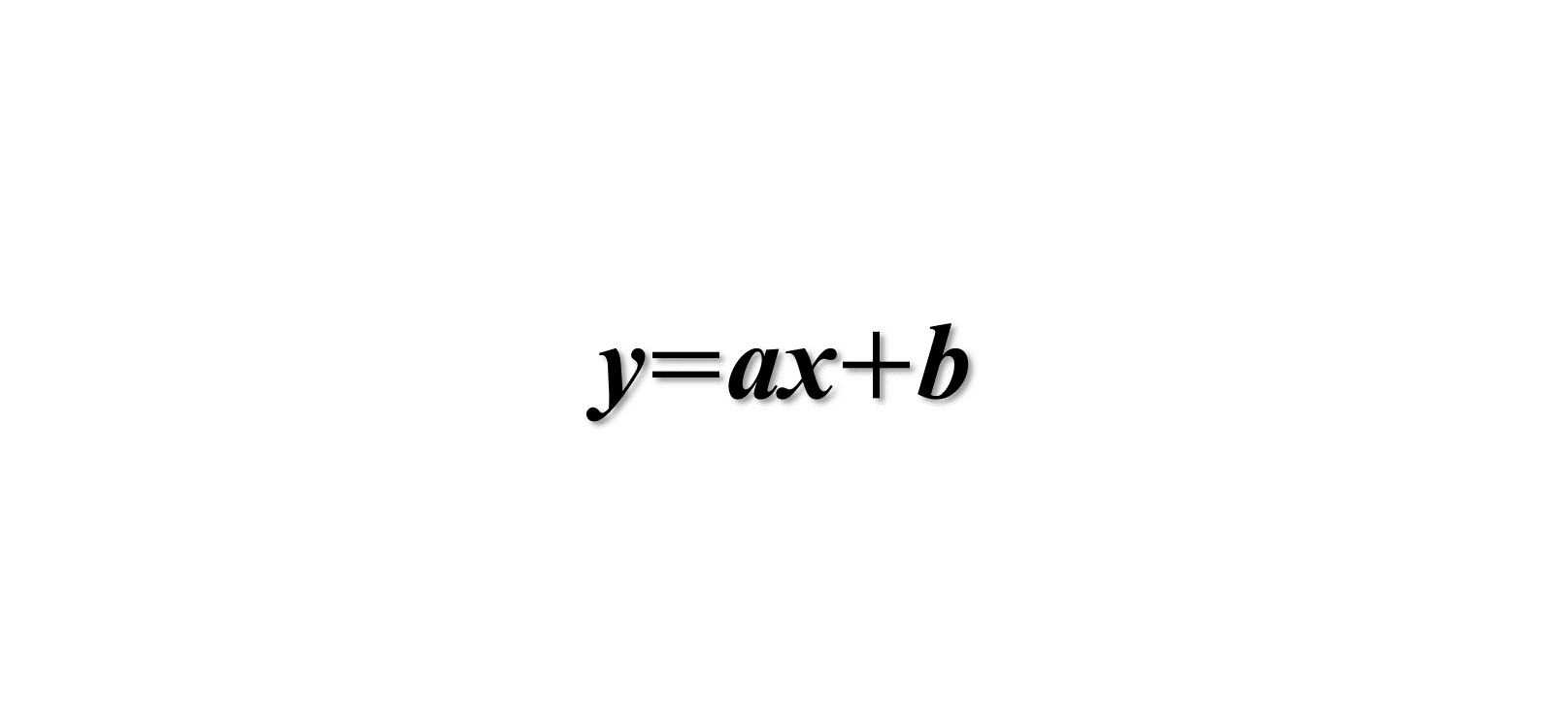

コメント